Puzzle ZURT 

Workings

Hint
What are the possible differences?

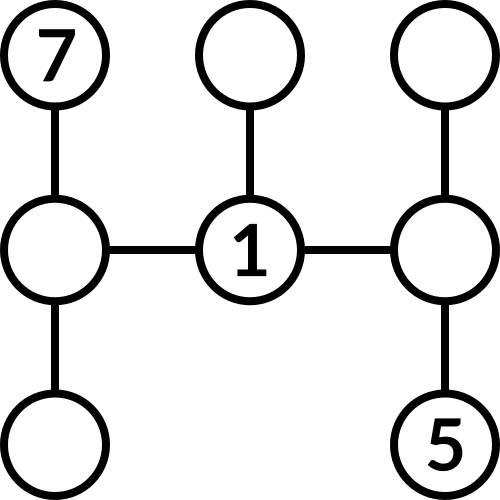
Answer
 


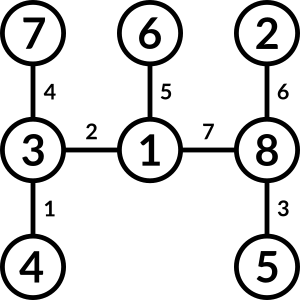
Reasoning
The first observation is that all of the possible gaps must exist: 1, 2, 3, 4, 5, 6, 7, and let's call these Gap1, ..., Gap7.

Looking at Gap7, this can only happen when:
   [Gap7a: 1 is next to 8]

Looking at Gap6, this can happen when:
   [Gap6a: 1 is next to 7]
      this is not allowed because 1 and 7 are given squares that are not next to each other.
   [Gap6b: 2 is next to 8]

Looking at Gap5, this can happen when:
   [Gap5a: 1 is next to 6]
   [Gap5b: 2 is next to 7]
      this is not allowed because [Gap6b: 2 is next to 8], which would mean that we can't also have [Gap7a: 1 is next to 8].
   [Gap5c: 3 is next to 8]
      this is not allowed because we couldn't then also have: [Gap7a: 1 is next to 8] and [Gap6b: 2 is next to 8].

We can't have the 8 above the 1, as there is then no place for [Gap6b: 2 is next to 8].

So, we have two possible places for the 8, to the left of the 1, or to the right of the 1.

8 to the left of 1



What can we place to the right of 1?

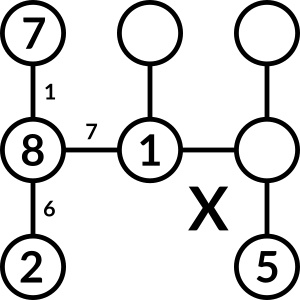
3 – no, because the gap between the 1 and 3, and the gap between 3 and 5, are both 2.
4 – no, because the gap between 4 and 5 is 1, which we already have.
6 – no, because the gap between 5 and 6 is 1, which we already have.

So the 8 can't go to the left of 1.

8 to the right of 1

We know [Gap5a: 1 is next to 6].

Let's try 6 to the left of 1. No matter where we place the 3 and 4 we end up with duplicate gaps. So this doesn't work.



So, the 6 must go above 1, but the 4 can't go to the left of 1 because of duplicate gaps. Therefore, this doesn't work either.



Which means that the final answer is: