Skyscrapers Help

Rules / Objectives Summary

• Complete the grid such that every row and column contains the numbers 1 to the size of the grid.
• Each row and column contains each number only once.
• The rules around the outside tell you how many skyscrapers you can see.
• You can't see a shorter skyscraper behind a taller one.

See the Walkthrough or Advanced Features for extra tips and tricks.

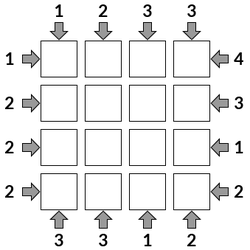
What are the numbers around the edges? Imagine standing around the edge, these numbers tell you how many skyscrapers you can see. You might be able to see any number from 1 up to the size of the grid. Move your mouse over the puzzle to see the answer.

Notes

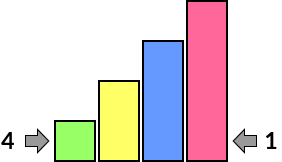
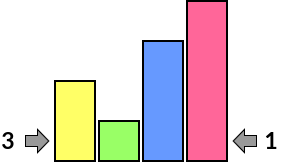
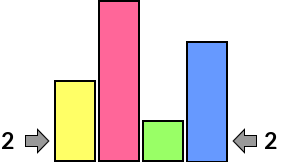
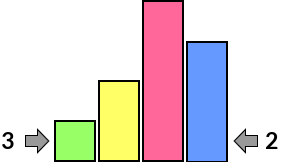
Here are a few examples of how the clues help us to see which skyscrapers we might be able to see:

Walkthrough

	Step 1 This is the start of the puzzle. Solve this puzzle for yourself at the same time.
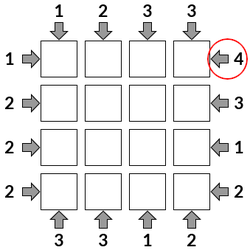
	Step 2 The 4 clue tells us that we can see all 4 skyscrapers, so they must be in order of size.
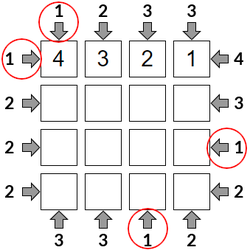
	Step 3 The 1 clue tells us that we can see only one skyscraper, which must be the <4>.
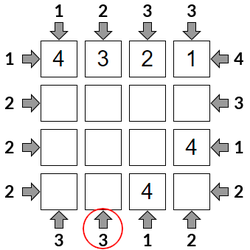
	Step 4 The 3 clue tells us that we can see three skyscrapers, which means that the <4> can't be first or second, and in fact the remaining <1>, <2>, <4> must be in order of size.
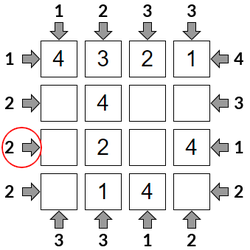
	Step 5 The 2 clue tells us that the first square can't be a <1> (otherwise we'd see 4 skyscrapers), so the first square must be the <3>.
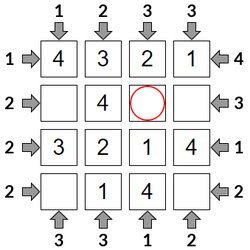
	Step 6 This is the only square for the <3> from Column 3.
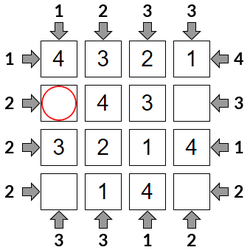
	Step 7 The <1> from Row 2 can't go in the last square as we already have a <1> in the end column, so this square must be the <1>.
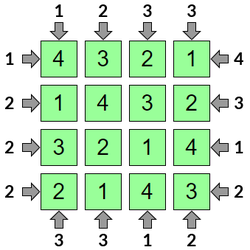
	Step 8 The puzzle now completes using the technique from Step 6.

Advanced Features

Skyscraper Puzzles share some similarities with the Sudoku puzzles and some of the advanced features are still available.

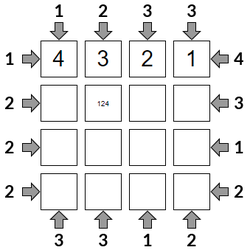
	Pencil Marks If you decide that a particular square could be two different numbers, you can enter them both, and the system will make the numbers smaller, just like pencil marks on a piece of paper.
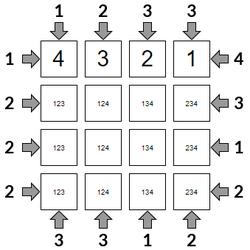
	Auto-Pencil Marks Pressing A (when your cursor is in the grid) will fill in all of the possible values for each square. If only one value remains, that square will take that value.
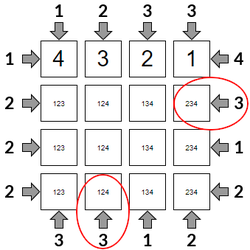
	Using Pencil Marks Once you have pencil marks these can be used for some advanced thinking. The highlighted squares cannot contain a <3> otherwise the we could never see three skyscrapers.
	Highlighting Numbers SHIFT+number will show all squares that contain that number as a pencil mark. In this puzzle we can see that there is only one place the <3> can go in Column 4.