??
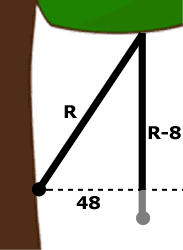
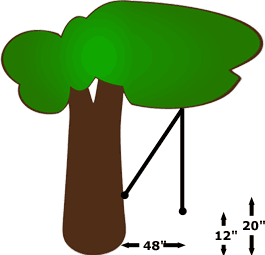
A rope swing hangs vertically down so that the end is 12 inches from the ground, and 48 inches from the tree.
If the swing is pulled across so that it touches the tree, it is 20 inches from the ground.
How long is the rope?
Puzzle Copyright © Elliott Line
This puzzle appeared in Mensa's EnigmaSig (198.24) and is used with permission.
Share link: https://www.brainbashers.com/
Note: BrainBashers has a Dark Mode option. For BrainBashers, I'd recommend not using your browser's built-in dark mode, or any dark mode extensions (sometimes you can add an exception for a specific website).