Puzzle 181
Chess Contest - Logic Puzzles
At the local games evening, four people were competing in the draughts and chess competitions.
Frankie beat Glen in chess, Dale came third and the 16 year old won.
Frankie came second in draughts, the 15 year old won, Dale beat the 18 year old and the 19 year old came third.
Emery is 3 years younger than Glen.
The person who came last in chess came third in draughts and only one person got the same position in both games.
Can you determine the ages of the people and their positions in the two games?
Puzzle Copyright © Kevin Stone
Share Link – www.brainbashers.com
Puzzle 182
Can you find anagrams of each of the words below? Each of the words has more than one anagram!
The initial letters of those new words also form an anagram.
Can you find the final word, which is related to the word QUESTION?
BRUISE
WARNED
PLEASE
LISTEN
VEINED
TRANCE
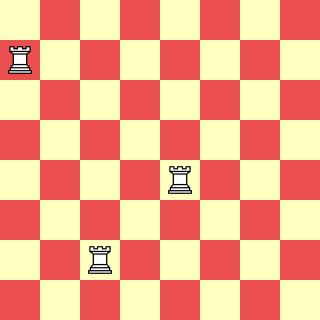
Puzzle Copyright © Kevin Stone
Share Link – www.brainbashers.com
Puzzle 183
Customer services at BrainBashers headquarters received the following letter recently.
Luckily our top puzzle solvers were able to determine the meaning and help Sam South.
Can you work out what the problem was?
D-a- K-v-n,
- ---ld l-k- -- c-m-la-n ab--- -h- --- --- -f m- ----------.
-h-s- l-----s d- n-- a---a- -- b- ---k-ng c----c-l-.
As --- can s--, -h-- a-- m-ss-ng f--m -h-s d-c-m-n-.
- ---ld b- v--- g-a--f-l -f --- c--ld c----c- -h-s ---bl-m -mm-d-a--l-.
K-nd --ga-ds.
Sam S---h.
Puzzle Copyright © Kevin Stone
Share Link – www.brainbashers.com
Puzzle 184
What number comes next in this sequence:
1 23 124 1251 26127 128129 {?}
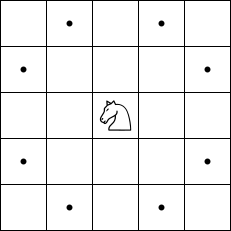
Puzzle Copyright © Kevin Stone
Share Link – www.brainbashers.com
Note: BrainBashers has a Dark Mode setting.