Puzzle 121
If a farmer buys chicken feed for £1.26 per tonne, pig feed for £2.74 per tonne and cattle feed for 78p per tonne. The feed can only be purchased by the tonne, and part tonnes aren't sold.
How much of each would he have if he had 100 tonnes for £100?
Puzzle Copyright © Kevin Stone
workings
hint
answer
print
Share link: https://www.brainbashers.com/puzzle/zokw
Answer
5 tonnes of chicken feed, 10 tonnes of pig feed and 85 tonnes of cattle feed.
Puzzle 122
Are there more seconds in a week …
… or feet in 100 miles?
Puzzle Copyright © Kevin Stone
workings
hint
answer
print
Share link: https://www.brainbashers.com/puzzle/zzld
Hint
There are three feet in a yard, and 1,760 yards in a mile.
Answer
Seconds in a week.
Reasoning
There are 60 x 60 x 24 x 7 = 604,800 seconds in a week.
There are 3 x 1760 x 100 = 528,000 feet in 100 miles.
Puzzle 123
What number replaces the question mark?
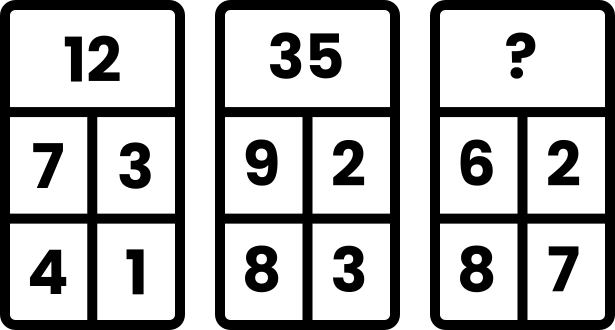
Puzzle Copyright © Kevin Stone
workings
hint
answer
print
Share link: https://www.brainbashers.com/puzzle/zwsm
Hint
In the first box, look at 7 & 3, and 4 & 1, to see how we can use them to make 12.
Answer
4.
Reasoning
For each row, the left minus the right gives a number.
The numbers for the rows are then multiplied together.
In the first box:
7 – 3 = 4
4 – 1 = 3
so 4 x 3 = 12
In the second box:
9 – 2 = 7
8 – 3 = 5
so 7 x 5 = 35
In the last box:
6 – 2 = 4
8 – 7 = 1
so 4 x 1 = 4.
Puzzle 124
As the auditor for my local theme park, I noticed that on Saturday there were 4,296 children and 2,143 adults and the takings were £98,718.
However, on Sunday, there were 5,146 children and 2,807 adults and the takings were £122,570.
How much were the children's tickets and adult's tickets?
Puzzle Copyright © Kevin Stone
workings
hint
answer
print
Share link: https://www.brainbashers.com/puzzle/zvhv
Hint
This is quite a tricky puzzle, and knowledge of algebra would certainly help.
Answer
The children tickets were £14, and the adult tickets were £18.
Reasoning
There are a number of methods for solving this problem, including:
Using a spreadsheet.
Using a computer program.
Using the intersection of lines on a graph.
Using an online equation solver.
Solving simultaneous equations using algebra.
Solving simultaneous equations using inverse matrices.
Here is my solution using simultaneous equations and algebra.
First construct two algebraic equations, where 'c' is the number of children, and 'a' is the number of adults:
[1] 4296c + 2143a = 98718
[2] 5146c + 2807a = 122570
To make the number in front of 'c' the same on both, we multiply [1] by 5146 and [2] by 4296 to give:
[3] 22107216c + 11027878a = 508002828
[4] 22107216c + 12058872a = 526560720
Now we can do [4] – [3] to give:
1030994a = 18557892
Divide throughout by 1030994 so that:
a = 18
Substituting a = 18 in [1] will give:
4296c + 2143 x 18 = 98718
4296c + 38574 = 98718
4296c = 60144
c = 14
Double-Checking
c = 14 and a = 18
4,296 x 14 + 2,143 x 18 = 98,718
and
5,146 x 14 + 2,807 x 18 = 122,570
< previous next >
Note: BrainBashers has a Dark Mode option. For BrainBashers, I'd recommend not using your browser's built-in dark mode, or any dark mode extensions (sometimes you can add an exception for a specific website).

