Puzzle 49
Yesterday I went for a short bicycle ride around the local lakes. As the weather was very hot, I rode in shorter stages than I'd normally ride.
In the first stage, I rode half of the overall distance.
Stage two saw half of the remaining distance plus 35 metres covered.
Stage three covered three-quarters of the remaining distance.
Stage four completed half of the remaining distance plus 75 metres.
Stage five completed the journey with a final burst of 150 metres.
How far did I cycle in total?
Puzzle Copyright © Kevin Stone
Share link:
Puzzle 50
The Miller next took the company aside and showed them nine sacks of flour that were standing as depicted in the sketch.
"Now, hearken, all and some," said he, "while that I do set ye the riddle of the nine sacks of flour.
And mark ye, my lords, that there be single sacks on the outside, pairs next unto them, and three together in the middle thereof.
By Saint Benedict, it doth so happen that if we do but multiply the pair, 28, by the single one, 7, the answer is 196, which is of a truth the number shown by the sacks in the middle.
Yet it be not true that the other pair, 34, when so multiplied by its neighbour, 5, will also make 196.
Wherefore I do beg you, gentle sirs, so to place anew the nine sacks with as little trouble as possible that each pair when thus multiplied by its single neighbour shall make the number in the middle."
As the Miller has stipulated in effect that as few bags as possible shall be moved, there is only one answer to this puzzle, which everybody should be able to solve.
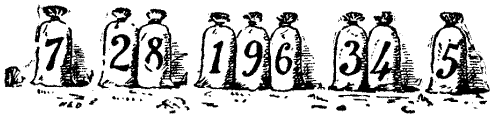
The Miller's Puzzle – The Canterbury Puzzles, Henry Ernest Dudeney.
Share link:
Puzzle 51
In the local wood there are a number of trees. On these trees there are a number of birds.
A local bird spotter knows that there are as many birds on each tree as there are trees in the wood, and that there are between 2000 and 2100 birds in total.
How many trees are there in the wood?
Puzzle Copyright © Kevin Stone
Share link:
Puzzle 52
In the illustration we have a sketch of Sir Edwyn de Tudor going to rescue his love, who was held captive by a neighbouring wicked baron.
Sir Edwyn calculated that if he rode at fifteen miles an hour he would arrive at the castle an hour too soon, while if he rode at ten miles an hour he would get there just an hour too late.
Now, it was of the first importance that he should arrive at the exact time appointed, in order that the rescue that he had planned should be a success, and the time of the tryst was five o'clock, when the captive would be taking afternoon tea.
The puzzle is to discover exactly how far Sir Edwyn de Tudor had to ride.
Sir Edwyn De Tudor – Amusements In Mathematics, Henry Ernest Dudeney.
Share link:
Note: BrainBashers has a Dark Mode option – I recommend not using your browser's dark mode or extensions for BrainBashers