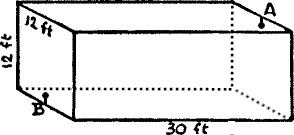
Here we have a rectangular room, measuring 30 feet by 12 feet, and 12 feet high.
There is a spider in the middle of one of the end walls, 1 foot from the ceiling (A).
There is a fly in the middle of the opposite wall, 1 foot from the floor (B).
What is the shortest distance that the spider must crawl in order to reach the fly?
The Spider and the Fly, The Canterbury Puzzles, Henry Ernest Dudeney.
workings
hint
answer
print
Share link: https://www.brainbashers.com/puzzle/zwql
Hint
Going down and across the floor isn't the only route.
Answer
40 feet.
Explanation Diagram
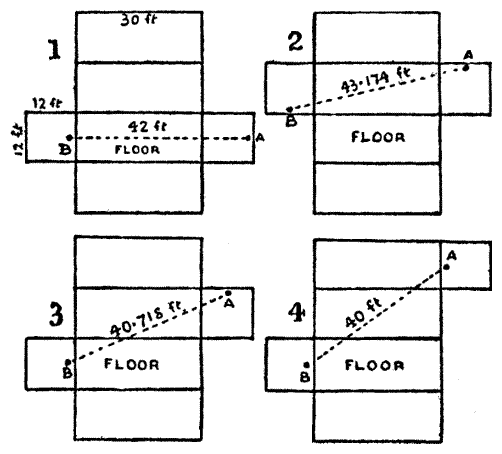
If you imagine the room to be a cardboard box, you can 'unfold' the room in various ways, and each route gives a different answer.
We can use Pythagoras' theorem (a2 + b2 = c2) to calculate the distances:
distance2 = horizontal2 + vertical2
distance = √(horizontal2 + vertical2)
Route #1
distance = 1 + 30 + 11 = 42 feet.
Route #2
horizontal = 6 + 30 + 6 = 42 feet.
vertical = 10 feet.
distance = √(422 + 102) ≈ 43.174 feet.
Route #3
horizontal = 1 + 30 + 6 = 37 feet.
vertical = 6 + 11 = 17 feet.
distance = √(372 + 172) ≈ 43.178 feet.
Route #4
horizontal = 1 + 30 + 1 = 32 feet.
vertical = 6 + 12 + 6 = 24 feet.
distance = √(322 + 242) = 40 feet.
Note: BrainBashers has a Dark Mode option. For BrainBashers, I'd recommend not using your browser's built-in dark mode, or any dark mode extensions (sometimes you can add an exception for a specific website).


