Objectives / Rules
- Eliminate numbers until there are no duplicate numbers in any row or column.
- Eliminate numbers by marking them in Black, and Black squares can't touch horizontally or vertically (diagonally is allowed).
- The remaining squares are White, and every White square can be reached from every other (i.e. they are connected).
See Getting Started and the Walkthrough below for extra tips and tricks.

What is the objective?
To eliminate duplicate numbers in the rows and columns.
You can only have (at most) one of any given number in each row and column (sometimes none).
Sometimes you don't have any of a given number in a row or column, and sometimes there are no Black squares in a row or column.
Click or move your mouse over the puzzle to see the answer.
Getting Started
Typical Start
In any row or column we are not allowed duplicates, so at least one of these squares must be Black. Therefore, the square between them must be White.
In any row or column we are not allowed duplicates, so at least one of these squares must be Black. Therefore, the square between them must be White.
Double In Row / Col
These numbers can't both be White, and they both can't be Black. Therefore, one of them is White, which means all other occurrences must be Black.
These numbers can't both be White, and they both can't be Black. Therefore, one of them is White, which means all other occurrences must be Black.
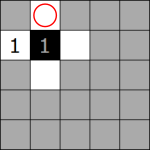
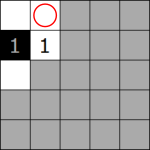
Double In Corner
When we have a double in a corner, one must be White and one must be Black. In both cases, this square must be White.
When we have a double in a corner, one must be White and one must be Black. In both cases, this square must be White.
Walkthrough


Step 2
As we're only allowed one <3> in Column 4, one of these squares must be Black. Whichever square that is, the square between the two must be White.
As we're only allowed one <3> in Column 4, one of these squares must be Black. Whichever square that is, the square between the two must be White.

Step 3
As we've now found a <5> in Column 4, all other <5>'s in the same Row or Column must be Black.
As we've now found a <5> in Column 4, all other <5>'s in the same Row or Column must be Black.

Step 4
All squares surrounding a Black one must be White.
All squares surrounding a Black one must be White.

Step 5
We've found a <3> in Column 3, so this square is Black (and those surrounding it are White).
We've found a <3> in Column 3, so this square is Black (and those surrounding it are White).

Step 6
This square is Black as we've already a <3> in Column 4.
This square is Black as we've already a <3> in Column 4.

Step 7
Since every White square can be reached from any other, this square must be White to avoid the <5> in the corner becoming isolated.
Since every White square can be reached from any other, this square must be White to avoid the <5> in the corner becoming isolated.

Step 8
We've already a <1> in Column 5, so this square is Black.
We've already a <1> in Column 5, so this square is Black.

Step 9
These squares must be White to avoid isolated White squares next to them.
These squares must be White to avoid isolated White squares next to them.

Step 10
These squares are Black as we've already a <4> in Row 3, and a <3> in Column 2.
These squares are Black as we've already a <4> in Row 3, and a <3> in Column 2.

Step 11
If this square was Black we would split the puzzle into two sections, and the White squares would be isolated from each other. So this square must be White to avoid this.
If this square was Black we would split the puzzle into two sections, and the White squares would be isolated from each other. So this square must be White to avoid this.

Step 12
This square must be Black as we've already a <1> in Column 2, and the puzzle will then complete.
This square must be Black as we've already a <1> in Column 2, and the puzzle will then complete.

Step 14
The completed puzzle.
The completed puzzle.
Note: BrainBashers has a Dark Mode option. For BrainBashers, I'd recommend not using your browser's built-in dark mode, or any dark mode extensions (sometimes you can add an exception for a specific website).