Puzzle 81
Below, 10 nine-letter words have been broken into chunks of three letters.
These chunks have been mixed up, no chunk is used twice and all of the chunks are used.
Can you determine the 10 original words?
RBR TIM SAG TEL LIG ENT
HEA DLI BLE WHI HTN FER
CAR AGE ESC ING IND WAT
TIL HAI USH DIF ETA NEW
RLW ALL ERF OPE ENT GHT
Puzzle Copyright © Kevin Stone
Share link – www.brainbashers.com

Puzzle 82
How many squares have been placed in the drawing below?
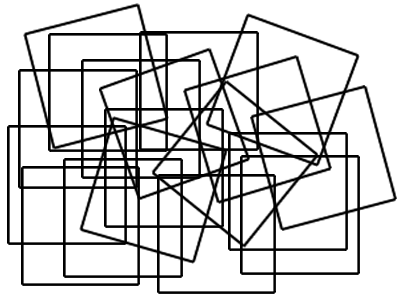
Puzzle Copyright © Kevin Stone
Share link – www.brainbashers.com
Puzzle 83
Last week I travelled from London to Leeds, a distance I measured as 174 miles.
I started at 9.15am and completed the journey with an average speed of 40 miles per hour.
On the way back, in the evening, I travelled exactly the same route, starting at 5.15pm. The traffic was light and I completed the journey with an average speed of 60 miles per hour.
What was the overall average speed for the round trip?
The answer is not 50 mph.
Puzzle Copyright © Kevin Stone
Share link – www.brainbashers.com
Puzzle 84
Can you find a five-digit number that has no zeros, and no digit is repeated, where:
The first digit is a prime number.
The second digit is the fifth digit minus the first digit.
The third digit is twice the first digit.
The fourth digit is the third digit plus three.
The fifth digit is the difference between the first digit and the fourth digit.
Don't forget that 1 isn't prime, but 2, 3, 5 and 7 are prime.
Puzzle Copyright © Kevin Stone
Share link – www.brainbashers.com
Note: BrainBashers has a Dark Mode setting.
