Puzzle 73
Marathon Warm-up – Logic Puzzles
After the recent BrainBashers annual marathon, the judges were comparing notes to determine who finished where. From their notes, can you help them reconstruct the final result?
Max Merrymood beat Toby Trent and Jesse Jackson.
Pat Piper beat Jesse Jackson, Toby Trent, and Alex Ardle.
Zeb Zebra lost to Pat Piper.
Glenn Goodfellow beat Toby Trent
Zeb Zebra beat Frankie Flint.
Glenn Goodfellow lost to Frankie Flint and Pat Piper.
Toby Trent beat Billie Brick.
Alex Ardle beat Zeb Zebra, Kelly Kingfisher, and Glenn Goodfellow.
Kelly Kingfisher lost to Glenn Goodfellow and Max Merrymood.
Billie Brick beat Kelly Kingfisher.
Max Merrymood lost to Alex Ardle and Zeb Zebra.
Frankie Flint beat Toby Trent, Max Merrymood, and Billie Brick.
Toby Trent lost to Jesse Jackson and Alex Ardle.
Jesse Jackson beat Glenn Goodfellow and Billie Brick.
Puzzle Copyright © Kevin Stone
www.brainbashers.com
Puzzle 74
Using all of the letters A to Z, each once only, complete these common words. There are currently 2 different answers, can you find them both?
ap--e
b-a-e
bo--d
-an-c
-ro-e
--ell
-ra-y
bu-c-
-o-ra
-umb-
s-ua-
lo--l
g-es-
Puzzle Copyright © Kevin Stone
www.brainbashers.com

Puzzle 75
Hidden in the grid below are six hidden animals.
The letters are in sequence, but you move from letter to letter using the moves of a chess knight.
Once you have crossed off all of the animals, you will be left with seven unused letters.
What animal do these letters spell?

The moves of a knight are:
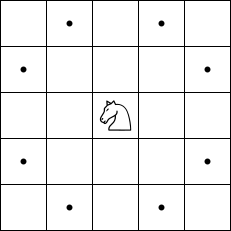
Note: this puzzle is not interactive, and the letters cannot be clicked.
Puzzle Copyright © Kevin Stone
www.brainbashers.com
Puzzle 76
During a recent trip to Scotland, I filled my car's 10 gallon fuel tank to the very top.
I travelled at 60 mph up the motorway, and I knew that I averaged exactly 40 miles per gallon.
However, the moment I started, my fuel tank developed a leak, and four hours later I came to a complete stop as I'd run out of fuel!
How much fuel did I lose through the leak?
Puzzle Copyright © Kevin Stone
www.brainbashers.com
