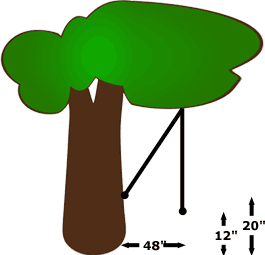
A rope swing hangs vertically down so that the end is 12 inches from the ground, and 48 inches from the tree.
If the swing is pulled across so that it touches the tree, it is 20 inches from the ground.
How long is the rope?
Puzzle Copyright © Elliott Line
This puzzle appeared in Mensa's EnigmaSig (198.24) and is used with permission.
workings
hint
answer
print
Share link – www.brainbashers.com/puzzle/zyjb
Hint
You might find Pythagoras' theorem very useful [a2 + b2 = c2].
Answer
148 inches.
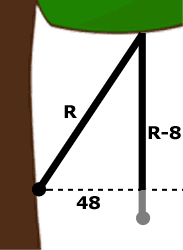
We can use Pythagoras' theorem if we draw an imaginary line across to create a right-angled triangle.
The hypotenuse is equal to the rope's length R. The bottom of the triangle is 48 inches. The vertical side is R - 8 (the difference between 20 inches and 12 inches).
Pythagoras' theorem tells us that:
a2 + b2 = c2
Where c is the hypotenuse.
This gives us:
482 + (R - 8)2 = R2
2304 + (R - 8)(R - 8) = R2
2304 + R2 - 16R + 64 = R2
2304 - 16R + 64 = 0
16R = 2368
R = 148
As required.


