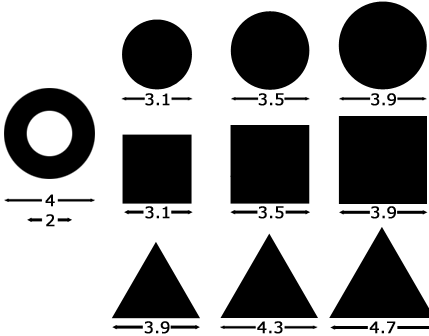Which square, which circle, and which triangle has the closest area to the doughnut shape on the left?
The drawings are to scale, so you might be able to judge it, as well as working the actual areas out.
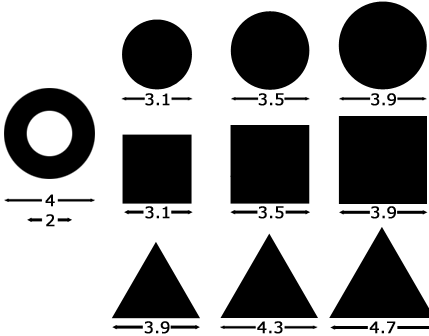
Puzzle Copyright © Kevin Stone
workings
hint
answer
print
Share link – www.brainbashers.com/puzzle/zkrc
Hint
The area of a circle is π x Radius2.
Answer
Circle: 3.5.
Square: 3.1.
Triangle: 4.7.
Doughnut
The area of a circle is π x Radius2.
The larger circle has diameter = 4, therefore the radius is 2, and the area is π x 22 = 4π.
The smaller circle has diameter = 2, therefore the radius is 1, and the area is π x 12 = π.
Therefore the shaded area is 4π - π = 3π ≈ 9.42.
Circle
The area of a circle is π x Radius2.
The circle with diameter 3.1 has a radius of 1.55 and an area of π x 1.552 = 7.55.
The circle with diameter 3.5 has a radius of 1.75 and an area of π x 1.752 = 9.62 (closest match).
The circle with diameter 3.9 has a radius of 1.95 and an area of π x 1.952 = 11.95.
Square
The area of a square is Side x Side.
The square with side 3.1 has an area of 3.1 x 3.1 = 9.61 (closest match).
The square with side 3.5 has an area of 3.5 x 3.5 = 12.25.
The square with side 3.9 has an area of 3.9 x 3.9 = 15.21.
Triangle
The area of a triangle is ½ x Base x Height. Using Pythagoras' theorem it can be shown that the area of an equilateral triangle is Sqrt(3) x Base2 ÷ 4.
The triangle with side 3.9 has an area of Sqrt(3) x 3.9 x 3.9 ÷ 4 = 6.59.
The triangle with side 4.3 has an area of Sqrt(3) x 4.3 x 4.3 ÷ 4 = 8.01.
The triangle with side 4.7 has an area of Sqrt(3) x 4.7 x 4.7 ÷ 4 = 9.57 (closest match).