Objectives / Rules
- Complete the grid such that every row and column contains the numbers 1 to the size of the grid.
- Every row and column contains each number exactly once.
- A cage clue tells you the answer after the cage values have undergone the specified mathematical operation.
- The clues don't tell you which way round the numbers are, just the answer to the calculation.
- A number can appear more than once in a cage (which is different to Killer Sudoku).
See the Walkthrough below for extra tips and tricks.
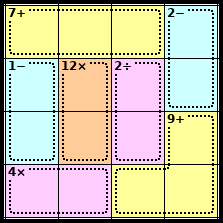
What are the little numbers and mathematical symbols for?
These tell you the answer when the digits in the cage undergo that mathematical operation.
Click or move your mouse over the puzzle to see the answer.
Walkthrough
Step 1
This is the start of the puzzle. This puzzle has a number of different answer methods, see if you can find another way of solving it.
Solve this puzzle for yourself at the same time.
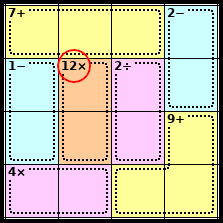
Step 2
The only way to make 12 in two squares using multiplication is 3 × 4.
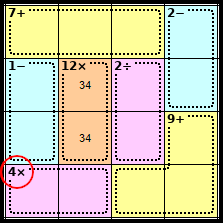
Step 3
The only way to make 4 in two squares using multiplication is 1 × 4 (as we can't have two 2's in the row).
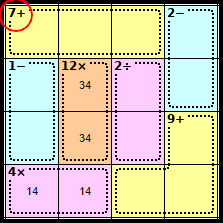
Step 4
The only way to make 7 in three squares using addition is 1 + 2 + 4.
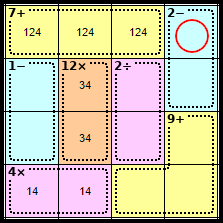
Step 5
As we know where the <1>, <2> and <4> of Row 1 are, we know that this square is <3>.
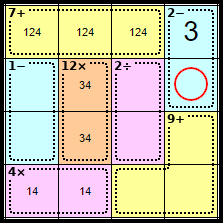
Step 6
As this cage must equal 2 under subtraction, it must be 3 - 1, which makes this square <1>.
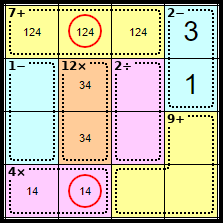
Step 7
Neither of these squares can contain <4>. This is because the 12× clue in this column MUST contain the <4>.
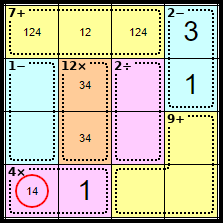
Step 8
Removing <4> on the previous step forced the <1> of this cage, which makes this square the <4>.
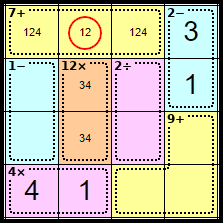
Step 9
As we now know where the <1> for this column is, we can remove it from this square leaving the <2>.
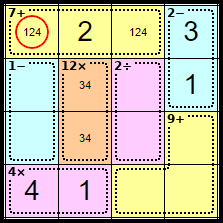
Step 10
As we now know where the <2> from Row 1 and the <4> for Column 1 are we can remove both of these from this square leaving <1>.
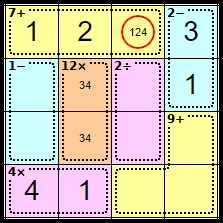
Step 11
Row 1 is only missing its <4>, and that must go in this square.
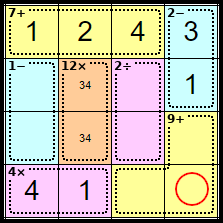
Step 12
This square can only be <2> as the other numbers are either in Row 4 or Column 4.
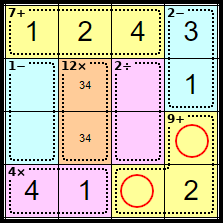
Step 13
Both of these numbers are forced as each only has one number left in the row or column.
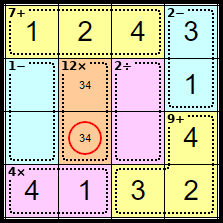
Step 14
As we know where the <4> for Row 3 is, we can remove it from this leaving the <3>, which forces the remaining square in Column 2 to be <4>.
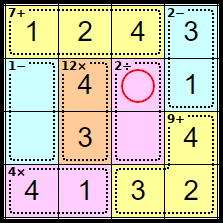
Step 15
This square can only be <2> as all other numbers already occur in the row or column.
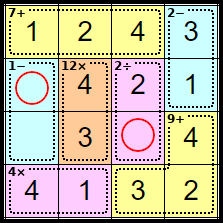
Step 16
These squares are now forced as each only has one number left in the row or column.
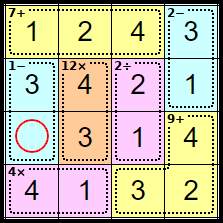
Step 17
There is only one number that this square can be, and the puzzle completes.
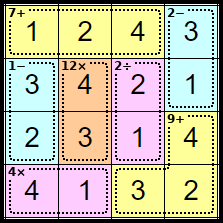
Step 18
The completed puzzle.
Note: BrainBashers has a Dark Mode option – I recommend not using your browser's dark mode or extensions for BrainBashers