Brain Teasers and Puzzles 

During the recent BrainBashers cipher convention, a Morse code contest took place.

The contest consisted of a Morse code transmission where the spaces between the letters and words were missing.

Can you decipher the sequence and find the well known proverb?

Luckily, BrainBashers has provided you with a listing of the Morse code characters:

Puzzle Copyright © Kevin Stone

workings hint answer print

Share Link – www.brainbashers.com/puzzle/zipy

The month of March in the year 1980 contained 5 Saturdays and 5 Mondays.

What day of the week was the 15th of March?

Puzzle Copyright © Kevin Stone

workings hint answer print

Share Link – www.brainbashers.com/puzzle/zvnz

Apparently, one side of a cat has more hair. The findings of the scientific establishment have been corroborated by a special enquiry by the BB Feline Federation. Many hair counts were taken of the side in question and consistently it was found to contain more hairs. The scientists determined that more hair was required on this side to insulate the cat from the elements while it was lying down. Perhaps you would like to examine a cat to confirm the findings. Before you do, can you guess which side of a cat has more hair?

workings hint answer print

Share Link – www.brainbashers.com/puzzle/zskv

The map below shows the street locations of a city. Position three police officers such that the entire length of every street can be seen by at least one officer.

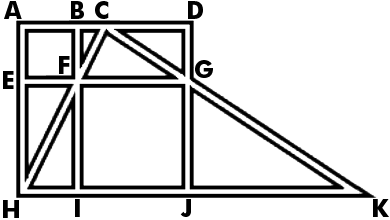
Puzzle Copyright © Cihan Altay

workings hint answer print

Share Link – www.brainbashers.com/puzzle/zmua